APLICACION DE LAS DERIVADAS EN LA ARQUITETURA

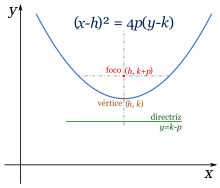
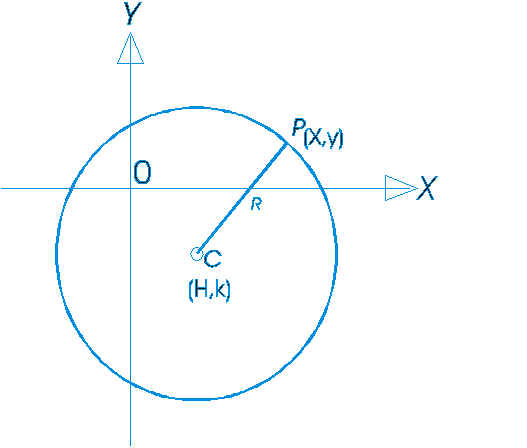
DERIVADAS.- es una medida de la rapidez con la que cambia el valor de dicha función matemática, según cambie el valor de su variable independiente.

Las derivadas tienen demasiadas aplicaciones, son la base e muchas de las ingenierías.

APLICACIONES DE LAS DERIVADAS

La derivada tiene una gran variedad de aplicaciones además de darnos la pendiente de la tangente a una curva en un punto. Se puede usar la derivada para estudiar tasas de variación, valores máximos y mínimos de una función, concavidad y convexidad, etc.

COMO POR EJEMPLO.

1. Un fondo de inversión genera una rentabilidad que depende de la cantidad de dinero invertida, según la formula: R(x)=-0.002x2+0.8x-5 donde R(x) representa la rentabilidad generada cuando se invierte la cantidad x. Determinar, teniendo en cuenta que disponemos de 500 dólares:



a) Cuando aumenta y cuando disminuye la rentabilidad

b) Cuanto dinero debemos invertir para obtener la máxima rentabilidad posible.

c) Cual será el valor de dicha rentabilidad.

Solución

a) La derivada primera nos da el crecimiento o decrecimiento de la función. Si la derivada es positiva la función crece y si es negativa decrece



Procedimiento:

-Se deriva la función:

R`(x)=-0,004x+0,8

-Se iguala a 0 y se resuelve la ecuación que resulta:


R`(x)=0




-Se estudia el signo de la derivada a la derecha e izquierda de los valores que nos ha dado 0 la derivada (en este caso x =200). Hay varios métodos, uno muy mecánico:




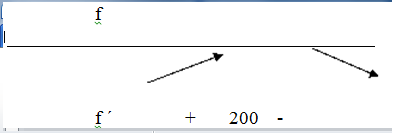
se coge un punto menor que 200, por ejemplo 100, y sustituimos R´(100)=0,4>0 y en otro mayor que 200 (por ejemplo 300) R´(300)=-0,4<0

Entonces la derivada es positiva en el intervalo (0, 200), y f es creciente en ese intervalo y es decreciente en (200, 500) ya que en ese intervalo nos ha dado negativa la derivada. Lo que nos dice también que en punto 200 hay un máximo local

b) Teniendo en cuenta el apartado a debemos invertir 200 euros.

c) La máxima rentabilidad es R(200)= -0,002.(200)2+0,8.200-5=75 euros

Calculo de máximos y minimos

En esta sección se muestra cómo usar la primera y segunda derivada de una función en labúsqueda de valores extremos en los llamados: “problemas de aplicaciones” o “problemas de optimización”. Aunque los ejemplos son esencialmente geométricos, ellosilustran un procedimiento general.

Se enumeran a continuación algunos pasos que son útiles al abordar un problema deesta naturaleza.
1. Hacer hasta donde sea posible un dibujo indicando las variables que intervienen en el problema.

2. Determinar la función a maximizar o minimizar asi como el intervalo en el cual está definida.

3. Utilizar la información del problema para expresar la función obtenida en el paso 2., en términos de una sola variable.

4. Utilizar la regla práctica dada en la observación al teorema 2 de la sección 9.9.3. para encontrar extremos absolutos.

EJERCICIOS:

Ejemplo 1.

Los puntos A y B están situados uno frente al otro y en lados opuestos de un rio recto de300 ms. de ancho. El punto D está a 600 ms. de B y en su misma orilla. (fig. 4.22).Una compañía de teléfonos desea tender un cable desde A hasta D. Si el costo por metro de cable es el 25% más caro bajo el agua que por tierra. ¿Cómo se debe tender el cable, para que el costo total sea mínimo?.






Solución:

Sea Q el punto sobre la misma orilla y a una distancia x de B donde termina el tramo de cable bajo el agua.

Se puede definir ahora las constantes y variables del problema:

x: distancia de B a Q; 0 ≤ x ≤ 600

y: distancia de A a Q; (longitud de cable bajo el agua).

600 – x: distancia de Q a D; (longitud de cable por tierra).

k (const): costo por metro de cable por tierra


(const): costo por metro de cable por agua.




P : costo total (función a minimizar).

De acuerdo al teorema de Pitágoras




Ahora, la función costo total viene dada por:



Sustituyendo (1) en (2), la función costo total puede escribirse en términos solamente de la variable x así:




Como C (x) es una función continua en un intervalo cerrado, C (x) alcanza un valor máximo y un valor mínimo en [0, 600].

Al derivar en (3) e igualar a cero, se obtienen los puntos críticos:







Asi que x = 400 es el único punto crítico y de acuerdo al criterio de la segunda derivada, corresponde a un mínimo relativo (verifíquelo). En consecuencia, el mínimo absoluto es el menor entre los siguientes valores: C (0), C (400) y C (600).



Esto significa geométricamente, que el cable se tira desde A hasta B bajo el agua y desde B hasta D por tierra, implicando un gasto de 975 k pesos

Esto indica geométricamente, que el punto Q coincide con D, y en este caso el cable se tiende directamente desde A hasta D por agua, demandando un gasto total de



Esto significa que si el punto Q está a 400 mts. de B y se tiende el cable bajo el agua desde A hasta Q y por tierra desde Q hasta D, demandaría un gasto de 825 k pesos, menor, para la compañía que los dos anteriores. (fig. 4.23 (c)).

fuente:

http://docencia.udea.edu.co/

APLICACIÓN DE LOS LIMITES EN LA ARQUITECTURA

El  uso de los limites describe se comportamiento de una función conforme la variable está muy aproximada a un valor constante o determinado valor. El limite se utiliza para el cálculo infinito, el cálculo de un cantidad infinitamente pequeña, en el que deben definirse estrictamente límites y considerarlos como números en la práctica. Se utiliza para definir los conceptos fundamentales de convergencia, derivación e integración, entre otros.

Es útil en los procesos económicos-administrativos para determinar producción y rendimiento al máximo. Como lo utilizamos en la resolución de problemas dadas las funciones en donde la variable no estaa especificada, se determina como  infinito, sirve para determinar costo promedio y producción máxima.

En el largo plazo, los limites sirven para que una cantidad se estabilice (temperatura, dinero, cantidades de reactivos, potencia, etc.

• Como pro ejemplo en la construcción:

Una caja cerrada, de base cuadrada tiene un volumen de 250 metros cuadrados. El material de las partes superior e inferior de la caja cuestan US$ 2 por metro cuadrado .e el de los lados US$ 1 por . Exprese el volumen de la caja como una función de la longitud de su base.

EJERCICIOS

Una compañía aérea de las denominadas “low-cost” ha establecido una línea

regular entre dos ciudades. Los estudios de mercado indican que la variación

de pasajeros que utilizarán dicha línea con el paso del tiempo, viene dada por:

a) Se sabe que a lo largo del primer año el número de personas que utilizará

los servicios de la compañía será creciente. ¿Ocurrirá lo mismo en los 3

años siguientes?

b   b) Podría ocurrir que la compañía, con el paso del tiempo, no obtuviese

Beneficios?

Solución

a) Se trata de averiguar si hay algún valor de t a partir del cual cambie el crecimiento de p(t). Para ello, resolvemos la ecuación  p´ (t) = 0, es decir, f( t) = 0 . Si e (1− t) = 0  , entonces t = 1. Por tanto, f (t) > 0 para  0<  t < 1 y para f(t )<0. En conclusión: durante el primer año el número de viajeros aumentará y, a partir de entonces, el número de viajeros que utilizará la línea descenderá.

b) Analizamos el límite de f( t) cuando t → +∞,

Puesto que el nº de viajeros, con el paso de los años, tiende a cero, sí puede ocurrir que, con el paso del tiempo, esta compañía aérea no fuera rentable.

Bibliografia.

https://www.google.com.ec

APLICACION DE LAS FUNCIONES EN LA ARQUITECTURA

FUNCIONES

ES una regla de asociación que relaciona dos o mas conjuntos entre si,  entre un conjunto llamado DOMINIO y otro llamado RANGO

Función lineal

 Las funciones lineales son polinomios de primer grado.    

Recordemos que los polinomios de primer grado tienen la variable elevada al exponente 1. Es habitual no escribir el exponente cuando este es 1.

Ejemplos de funciones lineales: a(x) = 2x+7        b(x) = -4x+3     f(x) =  2x + 5 + 7x - 3

De estas funciones, vemos que la f no está reducida y ordenada como las demás. Podemos reducir términos semejantes para que la expresión quede de una forma más sencilla,   f(x) =  9x + 2 

También recordemos que hemos convenido que cuando no establecemos en forma explicita el dominio y el condominio de una función, supondremos que es el mayor conjunto posible en cada caso.

Por ejemplo, si hablamos de la función f, de dominio real y condominio real, tal que f(x)= 2x-6, anotaremos  f: R ——-> R / f(x) = 2x-6 Siendo el dominio todos los números  reales, R, y el condominio también, todos los números reales, R.

Esto se lee " f de R en R tal que f de x es igual a 2x-6"

Vamos a graficar esta función, que tal cual lo vimos en la definición, es una función lineal por ser de primer grado.  Para graficarla haremos una tabla de valores.

f: R ——> R / f(x) = 2x-6

Le vamos dando valores a "x".   ¿Qué valores le podemos dar?  Cualquiera que este dentro del dominio.  

Por ejemplo, si x = 5 , entonces f(x) pasa a ser f(5), que es f(5) = 2.(5)-6        f(5) = 4

Entonces al 5 le corresponde el 4.   Nuestro punto es el (5,4).  

Función Logarítmica:

Se llama función logarítmica a la función real de variable real, 

• la función logarítmica solo esta definida sobre los números positivos
• los números negativos y el cero no tienen ningún logaritmo

Función trigonométrica:

Las funciones trigonométricas son las funciones establecidas con el fin de extender la definición de las razones trigonométricas a todos los números reales y complejos. Las razones trigonométricas se definen comúnmente como el cociente entre dos lados de un triángulo rectángulo asociado a sus ángulos.

 

APLICACIÓN

La matemática hace el diseño de edificios más seguro y más preciso. La trigonometría es especialmente importante en la arquitectura, ya que permite al arquitecto calcular las distancias y las fuerzas relacionadas con elementos de la diagonal. De las seis funciones de trigonometría básicas, el seno, el coseno y la tangente son los más importantes para la arquitectura, ya que permiten al arquitecto encontrar fácilmente los valores opuestos y adyacentes relacionados con un ángulo o la hipotenusa, la traducción de un vector diagonal en vectores horizontales y verticales.

Fuente

http://www.ehowenespanol.com/trigonometria-arquitectura-como_127481/

Aplicacion de las matrices en la arquitectura

Una matriz es la forma de organizar cierto numero de datos en un formato de manera que puedan relacionarse dichos datos entre si; la matriz de relaciones ponderada esta diseñada en un formato dividido en tres partes (una columna, casillas horizontales y casillas diagonales), en el cual se colocan los espacios del proyecto y por mediodel cual relacionamos entre sí todos los espacios que conformarán el proyecto arquitectónico. Establezcamos los tipos de relación, partiendo de los siguientes criterios:

Relación Necesaria: Es la relación indispensable entre dos o más espacios, implica una dependencia (funcional) total de un espacio con otro (sin el primero no funciona el segundo) hay un espacio que sirve y otro servido; ejemplo: comedor y cocina, el espacio que sirve es la cocina y el servido es el comedor; si no existe la cocina, quien sirve al comedor?. Condición: Los espacios con este tipo de relación

NUNCA se deben separar.

Relación Deseable: En este tipo de relación la dependencia no es total y la proximidad de los espacios es solamente “deseable” o conveniente, los espacios funcionan sin necesidad de la presencia del otro; ejem-plos: sala y garaje, comedor y despensa. Condición: Estos espacios pueden estar separa-dos por otro espacio (que podría ser un vestíbulo).

Relación Inexistente: Cuando no existe ningún tipo de relación entre los espacios, ejemplo: sala visitas y dormitorio de servicio. IMPORTANTE: En la matriz de relaciones no se colocan espacios de circulación (vestíbulos o pasillos) ni jardines.

1.Ordenamos la matriz

2. Se interrelaciones los espacios cruzandolo en las franjas diagonales

3. Seguidamente deben sumarse los valores contenidos

4. Se establecen rangos de acuerdo a las sumatorias obtenidas

Fuente: https://es.scribd.com/doc/104704046/diagramacion-en-arquitectura

APLICACIÓN DE LAS SECCIONES CÓNICAS EN LA ARQUITECTURA

ELIPSE

 

Se utiliza en la cconstrucción de anfiteatros, escaleras de caracol, en la superficie de cupulasya que permiten adoptar distintas formas segun el metodo de cconstrucción

Ejercicios de apicacion

• Hallar la ecuación de la elipse cuyos focos son los puntos $(-4,3)$ y $(4,3)$, con vértices $(-8,3)$, $(8,3)$. Haga un bosquejo de la gráfica. 

Solución:

Calculemos la medida del eje mayor y el centro de la elipse:

Eje mayor	$=$	Distancia de $V$ a $V\text{'}$
$2a$	$=$	$\sqrt{(-8-8}$ )2 +(3-3 )2
$2a$	$=$	$16$
$a$	$=$	$8$

Note que Centro $=(h,k)$ donde $k=3$ cálculemos el valor de $h$

Si $V\text{'}=(h+a,k)$ y temenos que $V\text{'}=(8,3)$:

$h+a$	$=$	$8$
$h+8$	$=$	$8$
$h$	$=$	$0$

Por lo tanto el centro de la elipse es el punto $(0,3)$. Además si $F\text{'}=(h+c,k)$ y $F\text{'}=(4,3)$ como $h$ es cero tenemos que $c=4$
Cálculemos $b$.

$b$	$=$	$\sqrt{a^2}$ - c2
$b$	$=$	$\sqrt{8^2}$ - 42
$b$	$=$	$48$
$b$	$\approx$	$6.9$

Finalmente sustituyendo en la ecuación de la elipse trasladada temenos:

$\frac{x^2}{}$ 64 + (y-3 )2 48 =1

                                                                                                                                                                   

PARABOLA

Todas ellas tienen una gran importancia para la arquitectura ya que la misma forma tiene una buena resistencia estructural y estética se utiliza con mayor frecuencia en arcos cupulas y puentes

Ejercicios de aplicación

  

• Qué ecuación tiene una parábola cuyo eje es paralelo al eje y sabiendo que pasa por el punto  y su vértice se halla en el punto ?

Solución

Calculamos p y para ello escribimos  Sabes que esta parábola pasa por el punto (4.5,1.5), sustituyendo en (I):

                                                                                                                                                                   

HIPERBOLA

    

 

sobre el eje x 

sobre el eje y

                           

   con centro (h,k)

:

                                                                            

Es el lugar geometrico de los puntos del plano tales que la diferencia de sus distancias a dos puntos fijos llamados focos siempre es constante y menor a la distancia entre los focos

Ejercicios de aplicacion

  

• Hallar la ecuación canónica, los focos, los vértices, la excentricidad y las asíntotas de la hipérbola cuya ecuación es

Solución:

Primer paso, se completa al cuadrado en ambas variables.

Por tanto, el centro está en . El eje de la hipérbola es horizontal,  y

Los vértices están en 
Los focos en 
La excentricidad es .

                                                                                                                                                                   

CIRCUNFERENCIA

     

      

                                                            

Ejercicios de aplicacion

 

• Calcula la ecuación de la circunferencia que tiene su centro en el punto de intersección de la rectas x + 3y + 3 = 0, x + y + 1 = 0, y su radio es igual a 5